Magnitudes escalares y vectoriales.
Las magnitudes son cualquier cosa que se pueda medir (velocidad, tiempo, temperatura…). Cuando medimos la temperatura de un objeto con un termómetro, el resultado de la medida posee significado pleno, sin necesidad de añadir nada más: la temperatura es 37 ºC. En estos casos, diremos que la magnitud es una magnitud escalar, y como ejemplos tenemos, además de la temperatura, la masa, la densidad, el tiempo, etc.Sin embargo, hay otras magnitudes físicas que necesitan, para estar plenas de sentido y significado, añadir otras descripciones a ese valor, por ejemplo, considérese la velocidad, si decimos que un coche circula a 45 km/h, sabemos cuánto espacio recorre en un determinado tiempo, pero no sabemos por dónde los recorre, ni hacia dónde lo hace: no será lo mismo que el coche circule por la SE-30 que por la calle Imagen, y a su vez, en la calle Imagen, podrá ir hacia La Campana, o hacia San Pedro. Estas magnitudes se llaman vectoriales, y en Física se determinan asignándoles un vector. En Matemáticas, un vector es un segmento orientado, que posee: un punto de aplicación, una dirección (recta sobre la que se asienta), un sentido (lado de la recta al que apunta la flecha), y un módulo (largo de la flecha, coincide con el valor numérico de la magnitud). En estos apuntes, los vectores se representan utilizando las negritas. La mayor parte de las magnitudes que se utilizan en cinemática son vectoriales, por ejemplo: velocidad, aceleración, momento lineal, etc. En este curso, aunque se realizarán algunas referencias puntuales al carácter vectorial de estas magnitudes, en general prescindiremos del mismo, y las tomaremos como escalares.
Magnitudes fundamentales y derivadas
Una magnitud fundamental es aquella que se define por sí misma, sin necesidad de ninguna otra, y se puede medir de forma directa. En el Sistema Internacional (SI) solo existen 7 magnitudes fundamentales:
Una magnitud derivada es la que resulta de una combinación de magnitudes fundamentales. Por ejemplo: superficie (producto de dos longitudes), densidad (masa por unidad de volumen) o velocidad (espacio por unidad de tiempo).
Ecuación de dimensiones
La ecuación de dimensiones expresa la relación de una magnitud derivada con las fundamentales. Cada magnitud fundamental se representa por una letra (ver arriba) elevada al exponente que resulte. Las constantes no tienen dimensiones. En cualquier expresión o ecuación científica, las dimensiones de ambos miembros deben ser iguales.Ejemplos de dimensiones de algunas magnitudes derivadas:
- Área: L·L=L2
- Volumen: L·L·L=L3
- Velocidad: L·T-1
- Aceleración:L·T-2
- Densidad: M·L-3
- Fuerza:M·L·T-2
- Potencia Eléctrica:M·L2·T-3·I-1
- Carga Eléctrica: I·T
Errores en la medida
Error sistemático vs error aleatorio
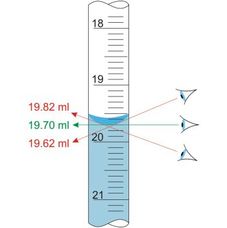
Error sistemático es aquel error que se comete siempre, por derivar de un problema del aparato de medida o por un defecto al emplearlo. Por ejemplo, un error de fabricación de una probeta produciría un error sistemático, y también sería un error sistemático el error de paralaje (no colocar el líquido a la altura de los ojos) al emplearla.
El error aleatorio es aquel que se da en condiciones idénticas pero que presentan desviaciones que no son previsibles respecto al verdadero valor. En otras palabras: es un error inevitable que se produce por eventos únicos imposibles de controlar durante el proceso de medición
Error absoluto vs error relativo
Son dos formas de expresar el error de una medida. El error absoluto es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
El error relativo es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. No tiene unidades.
Lección sobre errores: ENLACE
La notación científica es una manera de expresar un número de una forma simple los cuales pueden ser número grandes o números chicos. En ella se usan solo las cifras significativas, multiplicadas por la potencia de diez adecuada.
Por ejemplo, tenemos la siguiente cantidad:
En notación científica sería:

Enciclopediadetareas.net,. (2015). MAGNITUDES FUNDAMENTALES Y DERIVADAS - Enciclopedia de Tareas. Retrieved 18 September 2015, from http://www.enciclopediadetareas.net/2014/01/magnitudes-fundamentales-y-derivadas.html
Fisicapractica.com,. (2015). Magnitudes escalares y vectoriales - FisicaPractica.Com. Retrieved 18 September 2015, from http://www.fisicapractica.com/magnitudes.php
Flores, R. (2015). Medida y error. Fisicayquimicaenflash.es. Retrieved 18 September 2015, from http://fisicayquimicaenflash.es/eso/3eso/conceptos/errores.html
IES La Magdalena. Avilés. Asturias.,. (2015). Cifras significativas. Cálculo de errores.. Retrieved 18 September 2015, from http://web.educastur.princast.es/proyectos/fisquiweb/Apuntes/Apuntes2Fis/CifrasErrores.pdf
Jiménez, A. (2015). @RROBA LIBRE: 2.3. MAGNITUDES FUNDAMENTALES Y DERIVADAS.Revistaarrobalibre.blogspot.com.es. Retrieved 18 September 2015, from http://revistaarrobalibre.blogspot.com.es/2012/09/23.html
Machuca, M. (2009). FISICA: ECUACIONES DIMENSIONALES. Marinamachuca.blogspot.com.es. Retrieved 18 September 2015, from http://marinamachuca.blogspot.com.es/2009/03/ecuaciones-dimensionales.html
Perfil, V. (2009). FISICA: ECUACIONES DIMENSIONALES. Marinamachuca.blogspot.com.es. Retrieved 18 September 2015, from http://marinamachuca.blogspot.com.es/2009/03/ecuaciones-dimensionales.html
Tirado, A., & perfil, V. (2015). Aprende Fisica: .Magnitudes Fundamentales y Derivadas.Aprendefisika.blogspot.com.es. Retrieved 18 September 2015, from http://aprendefisika.blogspot.com.es/p/magnitudes-fundamentales-y-derivadas.html
Torres, J. (2015). Introducción a la teoría de errores. Universidad de Granada. Retrieved 18 September 2015, from http://www.ugr.es/~jtorres/teor_err.pdf
Vilavila, S. (2015). FORMULAS DE ECUACIONES DIMENSIONALES. Academia.edu. Retrieved 18 September 2015, from https://www.academia.edu/8327994/FORMULAS_DE_ECUACIONES_DIMENSIONALES
Error sistemático es aquel error que se comete siempre, por derivar de un problema del aparato de medida o por un defecto al emplearlo. Por ejemplo, un error de fabricación de una probeta produciría un error sistemático, y también sería un error sistemático el error de paralaje (no colocar el líquido a la altura de los ojos) al emplearla.

El error aleatorio es aquel que se da en condiciones idénticas pero que presentan desviaciones que no son previsibles respecto al verdadero valor. En otras palabras: es un error inevitable que se produce por eventos únicos imposibles de controlar durante el proceso de medición
Error absoluto vs error relativo
Son dos formas de expresar el error de una medida. El error absoluto es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
El error relativo es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. No tiene unidades.
Lección sobre errores: ENLACE
Expresión de resultados con error. Cifras significativas. Notación científica.
Podíamos definir las cifras significativas como aquellas que tienen significado (nos aportan información) sobre el resultado de una medición. Son significativas la cifra afectada por el error (último dígito) y las situadas a su izquierda, que no sean ceros. Las cifras significativas nos aportan una idea de la precisión de la medida. No tiene sentido incluir en el resultado de una medición más cifras significativas que las afectadas por el error (incertidumbre en la medida).La notación científica es una manera de expresar un número de una forma simple los cuales pueden ser número grandes o números chicos. En ella se usan solo las cifras significativas, multiplicadas por la potencia de diez adecuada.
Por ejemplo, tenemos la siguiente cantidad:
139000000000 cm.
En notación científica sería:
References
AulaFacil.com: Los mejores cursos gratis online,. (2015). Retrieved 18 September 2015, from http://www.aulafacil.com/cursos/l9895/ciencia/fisica/fisica-general-i-notaciones-cientificas-funciones-trigonometricas/notacion-cientificaEnciclopediadetareas.net,. (2015). MAGNITUDES FUNDAMENTALES Y DERIVADAS - Enciclopedia de Tareas. Retrieved 18 September 2015, from http://www.enciclopediadetareas.net/2014/01/magnitudes-fundamentales-y-derivadas.html
Fisicapractica.com,. (2015). Magnitudes escalares y vectoriales - FisicaPractica.Com. Retrieved 18 September 2015, from http://www.fisicapractica.com/magnitudes.php
Flores, R. (2015). Medida y error. Fisicayquimicaenflash.es. Retrieved 18 September 2015, from http://fisicayquimicaenflash.es/eso/3eso/conceptos/errores.html
IES La Magdalena. Avilés. Asturias.,. (2015). Cifras significativas. Cálculo de errores.. Retrieved 18 September 2015, from http://web.educastur.princast.es/proyectos/fisquiweb/Apuntes/Apuntes2Fis/CifrasErrores.pdf
Jiménez, A. (2015). @RROBA LIBRE: 2.3. MAGNITUDES FUNDAMENTALES Y DERIVADAS.Revistaarrobalibre.blogspot.com.es. Retrieved 18 September 2015, from http://revistaarrobalibre.blogspot.com.es/2012/09/23.html
Machuca, M. (2009). FISICA: ECUACIONES DIMENSIONALES. Marinamachuca.blogspot.com.es. Retrieved 18 September 2015, from http://marinamachuca.blogspot.com.es/2009/03/ecuaciones-dimensionales.html
Perfil, V. (2009). FISICA: ECUACIONES DIMENSIONALES. Marinamachuca.blogspot.com.es. Retrieved 18 September 2015, from http://marinamachuca.blogspot.com.es/2009/03/ecuaciones-dimensionales.html
Tirado, A., & perfil, V. (2015). Aprende Fisica: .Magnitudes Fundamentales y Derivadas.Aprendefisika.blogspot.com.es. Retrieved 18 September 2015, from http://aprendefisika.blogspot.com.es/p/magnitudes-fundamentales-y-derivadas.html
Torres, J. (2015). Introducción a la teoría de errores. Universidad de Granada. Retrieved 18 September 2015, from http://www.ugr.es/~jtorres/teor_err.pdf
Vilavila, S. (2015). FORMULAS DE ECUACIONES DIMENSIONALES. Academia.edu. Retrieved 18 September 2015, from https://www.academia.edu/8327994/FORMULAS_DE_ECUACIONES_DIMENSIONALES

No hay comentarios:
Publicar un comentario